The transformer architecture introduced by Ashish Vaswani and colleagues
Recently, researchers at Google AI successfully applied the transformer architecture to images
Self-Attention & Convolutional Layers
To point out the similarities and the differences between a convolutional layer and a self-attention layer, we first recall how each of them process an image of shape $$W \times H \times D_{\textit{in}}$$.
The mechanisms behind CNNs are very well understood, however lifting the transformer architecture from 1D (text) to 2D (image) necessitates having a good grasp of self-attention mechanics.
You can refer to Attention is All You Need
Convolutional Layer
A Convolutional Neural Netword (CNN) is composed of many convolutional layers and subsampling layers. Each convolutional layer learns convolutional filters of size $$K \times K$$, with input and output dimensions $$D_{in}$$ and $$D_{out}$$, respectively. The layer is parametrized by a 4D kernel tensor $$\mathbf{W}$$ of dimension $$K \times K \times D_{in} \times D_{out}$$ and a bias vector $$\mathbf{b}$$ of dimension $$D_{out}$$.
The following figure depicts how the output value of a pixel $$\mathbf{q}$$ is computed. In the animation, we consider each shift $$\Delta\!\!\!\!\Delta = [-\lfloor K / 2 \rfloor, ..., \lfloor K / 2 \rfloor]^2$$ of the kernel separately. This view might be unconventional, but it will prove helpful in the following when we will compare convolutional and self-attention layers.
Multi-Head Self-Attention Layer
The main difference between CNN and self-attention layers is that the new value of a pixel depends on every other pixel of the image. As opposed to convolution layers whose receptive field is the $$K\times K$$ neighborhood grid, the self-attention's receptive field is always the full image. This brings some scaling challenges when we apply transformers to images that we don't cover here. For now, let's define what is a multi-head self-attention layer.
A self attention layer is defined by a key/query size $D_k$, a head size $$D_h$$, a number of heads $N_h$ and an output dimenson $$D_{\textit{out}}$$. The layer is parametrized by a key matrix $$\mathbf{W}^{(h)}_{\!\textit{key}}$$, a query matrix $$\mathbf{W}^{(h)}_{\!\textit{qry}}$$ and a value matrix $$\mathbf{W}^{(h)}_{\!\textit{val}}$$ for each head $$h$$, along with a projection matrix $$\mathbf{W}_{\!\textit{out}}$$ used to assemble all heads together.
The computation of the attention probabilities is based on the input values $$\mathbf{X}$$. This tensor is often augmented (by addition or concatenation) with positional encodings to distinquish between pixel positions in the image. The hypothetical examples of attention proabilities patterns illustrate dependencies on pixel values and/or positions: uses the values of the query and key pixels, only uses the key pixel positional encoding, uses both the value of the key pixels and their positions.
Reparametrization
You might already see the similarity between self-attention and convolutional layers.
Let's assume that each pair of key/query matrices, $$\mathbf{W}^{(h)}_{\!\textit{key}}$$ and $$\mathbf{W}^{(h)}_{\!\textit{qry}}$$ can attend specifically to a single pixel at any shift $\mathbf{\Delta}$ (producing an attention probability map similar to Figure 1).
Then, each attention head would learn a value matrix $$\mathbf{W}^{(h)}_{\!\textit{val}}$$ analogous to the convolutional kernel $$\mathbf{W}_{\mathbf{\Delta}}$$ (both in green on the figures) for each shift $$\mathbf{\Delta}$$. Hence, the number of pixels in the receptive field of the convolutional kernel is related to the number of heads by $$N_h = K \times K$$.
This intuition is stated more formally in the following theorem (proved in our paper
Theorem
A multi-head self-attention layer with
The two most crucial requirements for a self-attention layer to express a convolution are:
- having multiple heads to attend to every pixel of a convolutional layer's receptive field,
- using relative positional encoding to ensure translation equivariance.
The first point might give the first explanation why multi-head attention works better than single-head. Regarding the second point, we next give insights on how to encode positions to ensure that self-attention can compute a convolution.
Relative Positional Encoding
A key property of the self-attention model described above is that it is equivariant to reordering, that is, it gives the same output independently of how the input pixels are shuffled. This is problematic for cases we expect the order of input to matter. To alleviate the limitation, a positional encoding is learned for each token in the sequence (or pixel in an image), and added to the representation of the token itself before applying self-attention.
The attention probabilites (Figure 3, top right) are computed based on the input values and the positional encoding of the layer input. We have already seen that each head can focus on different part (position or content) of the image for each query pixel. We can explicitly decompose these different dependencies as follows:
Because the receptive field of a convolution layer does not depend on the input data, only the last term is needed for the self-attention to emulate a CNN.
An important property of CNN that we are missing is equivariance to translation.
This can be achieved by replacing the absolute positional encoding by relative positional encoding $$\mathbf{r}_\mathbf{\delta}$$.
This encoding was first introduced by Zihang Dai and colleagues in TransformerXL
In this manner, the attention scores only depend on the shift and we achieve translation equivariance. Finally we show that there exists a set of relative positional vectors of dimension $$D_{\textit{pos}} = 3$$ along with self-attention parameters that allow attending to pixels at arbitrary shift (Figure 1). We conclude that any convolutional filter can be expressed by a multi-head self-attention under conditions stated in the theorem above.
Learned Attention Patterns
Even though we proved that self-attention layers have the capacity to express any convolutional layer, this does not necessarily mean that the behavior occurs in practice. To verify our hypothesis, we implemented a fully-attentional model of 6 layers, with 9 heads each.
We trained a supervised classification objective on CIFAR-10 and reached a good accuracy of 94% (not state of the art, but good enough).
We re-used the learned relative positional encoding from Irawn Bello and colleagues
The attention probabilities displayed on Figure 4 show that, indeed, self-attention behaves similarly to convolution. Each head learns to focus on different parts of the images, important attention probabilities are in general very localized.
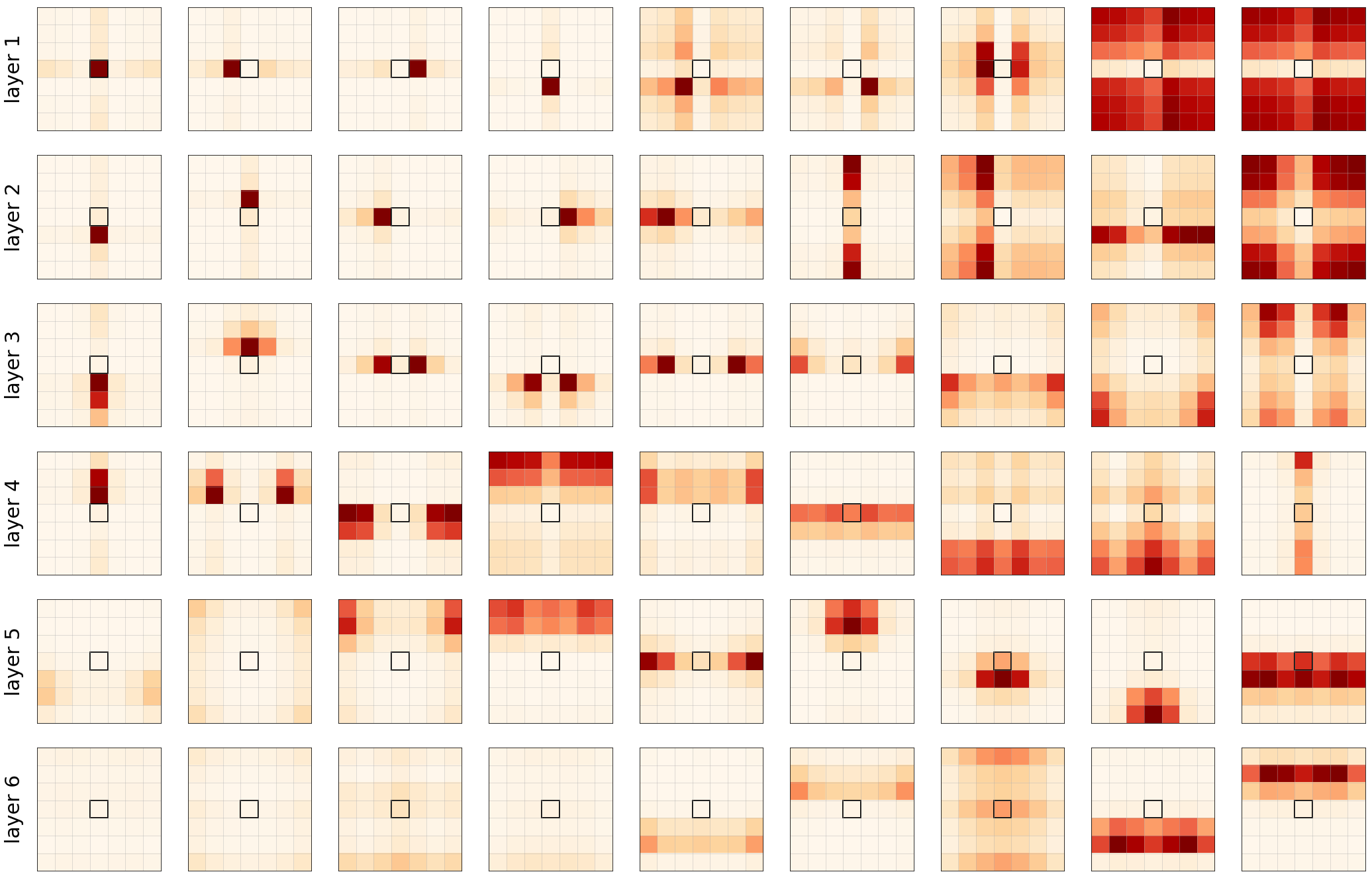
We can also observe that the first layers (1-3) concentrate on very close and specific pixels while deeper layers (4-6) are attending on more global patches of pixels over whole regions of the image. In the paper, we further experimented with more heads and obserded more complex (learned) patterns than a grid of pixels.
Conclusion
In our paper On the Relationship between self-attention and Convolutional Layers